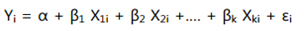회귀분석(Regression Analysis)
태그 :
- 개념
- - 원인이 되는 값과 결과가 되는 값의 상관관계를 통계적 기법에 의해 상관관계를 분석하는 대표적인 분류 기법
Ⅰ. 대표적인 분류분석 기법, 회귀분석(Regression Analysys) 의 개요
가. 회귀분석의 정의
- 원인이 되는 값과 결과가 되는 값의 상관관계를 통계적 기법에 의해 상관관계를 분석하는 대표적인 분류 기법
Ⅱ. 회귀분석의 유형
가. 독립변수의 수에 따른 유형
|
독립변수 수 |
유형 |
회귀식(사례) |
|
독립변수 1개 |
단순회귀분석 Simple Regression Analysis |
|
|
독립변수 2개 이상 |
다중회귀분석 Multiple Regression Analysis |
|
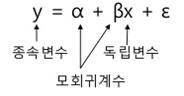
* y=절편, ß는 기울기로, 독립변수 1개를 가지는 회귀식은 기울기가 있는 직선의 상관관계를 가짐.
나. 종속변수의 수에 따른 유형
|
종속변수 수 |
유형 |
|
종속변수 1개 |
일변량 회귀분석 Univariate Regression Analysis |
|
종속변수 2개 이상 |
다변량 회귀분석 Multivariate Regression Analysis |
다. 종속변수의 형태에 따른 유형
|
연속형 |
범주형(이산형) |
|
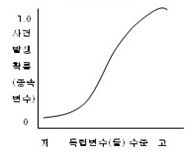
종속변수 Y가 확률값을 갖는 연속형 변수 |
종속변수 Y가 범주형(이산형) 변수 |
|
회귀분석(Regression Analysis) 직교회귀분석(Orthogonal Regression Analysis) |
로지스틱 회귀분석 Logistic Regression Analysis |
|
|
|
- 직교회귀분석은 종속변수 Y값과 방정식간의 직각거리를 최소화하는 분석기법 이며, 로지스틱 회귀분석은 종속변수가 2개 이상인 다항 로지스틱 회귀분석과 분화 로지스틱 회귀분석으로 분류됨.
Ⅲ. 변수와 관계의 이해
가. 변수의 이해
|
독립변수 |
종속변수 |
|
설명변수 |
반응변수 |
|
예측변수 |
목표변수 |
|
방정식에서 X 값 |
방정식에서 Y값 |
|
Input |
output |
이제 어떤 이름으로 나오더라도 독립변수와 종속변수를 구분할 수 있음
나. 관계의 이해
|
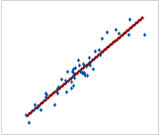
선형관계 |
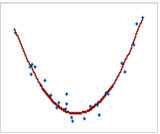
비선형관계 |
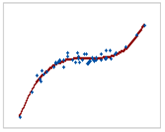
단조관계 |
|
|
|
|
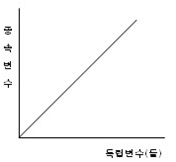
- 선형관계는 위와 같이 우측으로 가면서 높아지는 양의 선형관계와 반대로 우측으로 가면서 낮아지는 음의 선형관계가 있음
- 단조관계는 독립변수와 종속변수가 동시에 증가하기는 하지만 같은 비율로 증가하지 않음
IV.회귀식의 과적합을 막기 위한 정규화 선형회귀
가. 정규화 선형회귀(Regularized Linear Regression)의 개념
- 선형회귀 계수(weight)에 대한 제약 조건을 추가함으로써 모형이 과도하게 최적화되는 현상, 즉 과최적화를 막는 회귀분석 기법
나. 정규화 선형회귀의 유형
|
유형 |
설명 |
Pythons함수명 |
|
Ridge |
가중치들의 제곱합(squared sum of weights)을 최소화하는 것을 추가적인 제약 조건으로 하는 정규화 선형회귀 기법 |
Ridge() |
|
LASSO |
Lasso(Least Absolute Shrinkage and Selection Operator) 가중치의 절대값의 합을 최소화하는 것을 추가제약 조건으로 하는 정규화 선형회귀 기법 |
LASSO() |
|
Elastic Net |
가중치의 절대값의 합과 제곱합을 동시에 최소화 하는 것을 추가 제약 조건으로 하는 정규화 선형회귀 기법 |
ElasticNet() |