의사결정트리(Decision Tree)
태그 :
- 개념
- - 분류함수를 의사결정규칙으로 표현할 때 타원(분기점), 직선(가지), 사각형(잎사귀)을 이용하여 나무형태로 그려서 분석하는 기법
Ⅰ. 의사결정트리(Decision Tree) 의 개요
가. 의사결정트리(Decision Tree) 의 정의
- 분류함수를 의사결정규칙으로 표현할 때 타원(분기점), 직선(가지), 사각형(잎사귀)을 이용하여 나무형태로 그려서 분석하는 기법
- 규칙을 바탕으로 순서도고 구축한 이진트리
나. 의사결정트리의 특징
|
통계학 기반 |
- 평균, 확률 등의 통계학 개념을 기반으로 규칙 생성 |
|
트리 모형 |
- 트리 모형을 기반으로 규칙을 세분화 |
|
분류 목적 |
- 주어진 데이터를 분류(Classification)하는 목적으로 사용 |
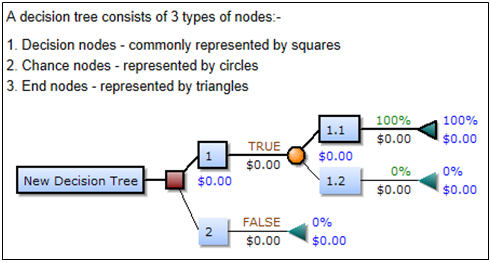
Ⅱ. 의사결정트리의 구성
가. 의사결정트리의 구성도 예시
|
|
나. 의사결정트리 구성요소
|
구성요소 |
설명 |
비고 |
|
노드 node |
- 분류를 위한 중요한 변수 - 최상위 노드를 뿌리 노드(root node)라 함 |
분기점 |
|
가지branch |
- 의사결정규칙에 사용된 변수의 경우의 수 |
규칙 반영 |
|
리프노드 leaf node |
- 최종분류 집단 |
하위 노드 없음 |
Ⅲ. 의사결정트리의 형성과정 및 알고리즘 사례
가. 의사결정트리의 형성과정
|
분석단계 |
상세 활동 |
|
의사결정나무형성 |
분석 목적과 자료구조에 따라 적절한 분리 기준(Split Criterion) 및 정지규칙(Stopping Rule) 지정 |
|
가지치기 |
분류오류(Classification Error) 유발 위험(Risk)이 높거나 부적절한 규칙을 가지는 가지(Branch) 제거 |
|
타당성 평가 |
이익도표(Gains Chart), 위험도표(Risk Chart), 검정 자료(Test Data)에 의한 교차타당성(Cross Validation) 등 이용, 의사결정나무 평가 |
|
해석 및 예측 |
의사결정나무의 해석, 분류 및 예측 모형 설정 |
- 정지/분리/평가 기준에 따라 다른 의사결정 나무 형성
나. 의사결정트리 기반의 알고리즘 사례
|
종류 |
설명 |
|
CHAID |
카이제곱 검정(범주형 목표변수) 또는 F-검정(연속형 목표변수)을 이용하여 다지분리(Multiway Split)를 수행하는 알고리즘 - 목표변수 별 분류기준 * 범주형 :우도비카이제곱 통계량, 카이제곱 통계량 * 순서형 :우도비카이제곱 통계량 * 연속형 :우도비카이제곱 통계량 |
|
CART |
지니 지수(Gini Index, 범주형) 또는 분산의 감소량(연속형)을 이용하여 이진분리(Binary Split)를 수행하는 알고리즘 지니지수(Gini Index) * 순도(Impurity)측정 지수 * n개의 원소 중 임의 2개 추출 시, 서로 다른 그룹에 속할 확률 |
|
C5.0 |
ID3라는이름의알고리즘으로만들어졌다가 1993년에 C4.5를거쳐 1998년에완성된알고리즘 * 장점 :가장정확한분류알고리즘 * 단점 :명목형목표변수만지원 |
다. 의사결정 알고리즘 비교
|
알고리즘 |
평가지수(선택방법) |
비고 |
|
ID3 |
Entropy |
다지분리(범주) |
|
C4.5 |
Information Gain |
다지분리(범주)및 이진분리(수치) |
|
C5.0 |
Information Gain |
C4.5와 거의 유사 |
|
CHAID |
카이제곱(범주), F검정(수치) |
통계적 접근 방식 |
|
CART |
Gini Index(범주), 분산의 차이(수치) |
통계적 접근 방식, 항상 2진 분리 |
Ⅳ. 의사결정트리의 장단점
|
장점 |
단점 |
|
모형의 이해도 쉬움 |
최적해를 보장하지 못함(greedy 알고리즘) |
|
두개 이상의 변수가 결과에 어떤 영향을 주는지 파악가능 |
비연속성 분류 |
- 새로운 자료의 예측은 어렵지만, 이해가 쉽고 활용도가 높음