몬테카를로 트리 서치 (Monte Carlo Tree Search)
태그 :
- 개념
- - 모든 트리 노드를 대상으로 하는 대신 게임 시뮬레이션을 통해 가장 가능성이 높아 보이는 방향으로 행동을 결정하는 탐색 방법
Ⅰ. AlphaGo의 게임 탐색 알고리즘 몬테카를로 트리 탐색(MCTS : Monte-Calro Tree Search)
가. 몬테카를로 트리 탐색의 정의
- 모든 트리 노드를 대상으로 하는 대신 게임 시뮬레이션을 통해 가장 가능성이 높아 보이는 방향으로 행동을 결정하는 탐색 방법
- 어떻게 움직이는 것이 가장 유망한 것인가를 분석하면서 검색 공간에서 무작위 추출에 기초한 탐색 트리를 확장하는 데 중점을 둔 트림 탐색
- 모종의 의사 결정을 위한 체험적 탐색 알고리즘으로, 특히 게임을 할 때에 주로 적용되며. 선두적 예로 컴퓨터 바둑 프로그램이 있으나, 다른 보드 게임, 실시간 비디오 게임, 포커와 같은 비결정적 게임에도 사용
Ⅱ. 몬테카를로 트리 탐색의 알고리즘 및 4단계 과정
가. 몬테카를로 트리 탐색의 알고리즘
|
|
- 깊이우선탐색 원리로, 선택-확장-시뮬레이션-역전파를 반복하는 탐색 알고리즘
나. 몬테카를로 트리 탐색의 4단계 과정
|
① 선택 |
현재 바둑판 상태에서 특정 경로로 수읽기를 진행 |
|
② 확장 |
일정 수 이상 수읽기가 진행되면 그 지점에서 한 단계 더 착수 지점을 예측(게임 트리의 확장) |
|
③ 시뮬레이션 |
②에서 선택한 노드에서 바둑이 종료될 때까지 무작위(random) 방법으로 진행. 속도가 빠르기 때문에 여러 번 수행할 수 있으나 착수의 적정성은 떨어짐 |
|
④ 역전파 |
③의 결과를 종합하여 확장한 노드의 가치(②에서 한 단계 더 착수한 것의 승산)를 역전파하여 해당경로의 승산 가능성을 갱신 |
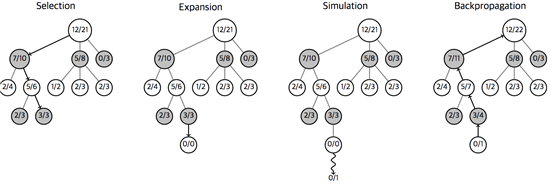
- 몬테카를로 트리 순회의 각 단계의 예 : 선택, 확장, 시뮬레이션, 역전파
1. 선택 (Selection) : 루트 R에서 시작하여 연속적인 자식 노드를 선택해 내려가 마디 L에 이른다. 몬테카를로 트리 탐색의 본질인, 게임 트리를 가장 승산 있는 수로 확장시킬 자식 노드를 선택하는 방법은 아래 난을 참고한다
2. 확장 (Expansion) : 노드 L에서 승패를 내지 못하고 게임이 종료되면, 하나 또는 그 이상의 자식 노드를 생성하거나 자식 노드중 노드 C를 선택한다
3. 시뮬레이션 (Simulation) : 노드C로부터 무작위의 플레이아웃을 실행한다
4. 역전파 (Backpropagation) : 플레이아웃의 결과로 C에서 R까지의 경로에 있는 노드들의 정보를 갱신한다
III. 몬테카를로 트리 탐색 핵심요소
가. 정책과 가치
|
정책 |
- 트리의 폭을 제한하는 역할 - MCTS의 두 번째 단계인 확장에서 주로 사용되는 것으로, 특정 시점에서 가능한 모든 수 중 가장 승률이 높은 것을 예측 |
|
가치 |
- 트리의 깊이를 제한하는 역할 - 가치는 현재 대국상황의 승산을 나타낸 것으로, 승산이 정확할 수록 많은 수(더 깊은 노드)를 볼 필요가 없음 |
12.1.1 바둑에서 정책은 전문가의 전략이 될 수도 있고, 과거 기본 데이터에서 많은 프로 기사들이 선호한 패턴이 될 수도 있음 (선호되는 방향을 정의)
12.1.2 가치는 바둑 국면의 형세판단을 근사하여 수치화한 것으로 볼 수 있음.
12.1.3 정확한 값은 모든 경우의 수를 계산하여 게임 종료 시점까지 가봐야 하기 때문에 계산이 어려움
12.1.4 MCTS에서 정책은 정확한 가치를 추정하는데 중요한 역할을 함. 정책은 게임의 미래 상태를 예측하기 때문에 게임의 특성과 경험을 반영
12.1.5 만약 정책이 최적화(optimize)하는 방향으로 수렴(converge)한다면, 가치 역시 최적의 값으로 수렴한다고 볼 수 있음 (i.e. 다음 착수가 가장 최적화된 방향이 라면 경기에 승리할 확률이 높아짐)
나. 보다 효율적인 정책과 가치 구현
12.1.6프로기사의 기본을 바탕으로 정책과 가치를 제안
12.1.7스스로 대국하는 학습기법을 통해 정책과 가치의 성능을 향상
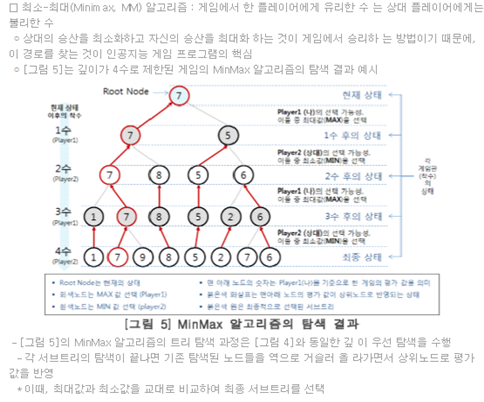
[참고1] MIN-MAX 알고리즘 (출처: http://honeybadger333.tistory.com/archive/20160624)

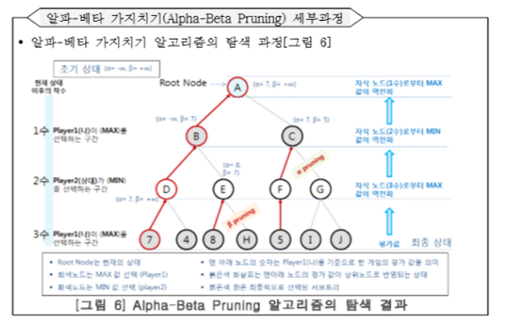
[참고2] Alpha-Beta Prunning 알고리즘 (출처: http://honeybadger333.tistory.com/archive/20160624)