Apriori 알고리즘
태그 :
- 개념
- - 데이터들에 대한 발생 빈도를 기반으로 각 데이터 간의 연관관계를 밝히기 위한 방법 - 구현이 간단하고 성능 또한 만족할 만한 수준을 보여주는 알고리즘으로 패턴 분석을 위해 자주 이용되는 알고리즘 - Apriori는 K번째 항목집합이 K+1번째 항목집합을 발견하기 위해 사용되는 레벨단위로 진행되는 반복 접근법을 사용
Ⅰ. Apriori 알고리즘의 개요
- 데이터들에 대한 발생 빈도를 기반으로 각 데이터 간의 연관관계를 밝히기 위한 방법
- 구현이 간단하고 성능 또한 만족할 만한 수준을 보여주는 알고리즘으로 패턴 분석을 위해 자주 이용되는 알고리즘
- Apriori는 K번째 항목집합이 K+1번째 항목집합을 발견하기 위해 사용되는 레벨단위로 진행되는 반복 접근법을 사용
Ⅱ. Apriori 알고리즘의 연관규칙 탐색 과정
가. 빈발 항목 집합(Large Itemset) 탐색
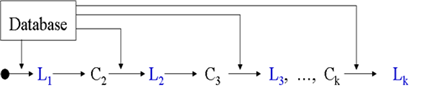
- 빈발 항목 집합을 찾는 것은 기본적으로 [그림-1]와 같은 과정.
- Database로부터 후보 항목 집합(Candidate Itemset)을 생성하고, 이를 데이터베이스 트랜잭션과 비교하여 빈발 항목 집합(Large Itemset)을 찾아내는 과정, 더 이상의 빈발 k-항목 집합이 없을 때까지 반복하는 과정을 거친 후 최종 빈발 항목 집합을 생성함
Lk: Set of Large k-itemsets, Ck: Set of Candidate k-itemsets
그림-1] 빈발 항목 집합 탐색 과정
[
- 빈발 항목 집합들(Large Item Sets)을 찾기 위해서 미리 결정된 최소 지지도(Minimum Support) 이상의 트랜잭션 지지도를 가지는 항목 집합들의 모든 집합들을 빈발 항목 집합들이라고 하며 그 외 모든 항목 집합들은 작은 항목 집합들(Small Itemsets)이라 함.
나. 연관 규칙 생성
- 데이터베이스로부터 연관 규칙을 생성하기 위하여 빈발 항목 집합을 이용. 지지도(Support)와 신뢰도(Confidence)는 다음의 식을 통해 계산
[표-1] X => Y 일때 지지도와 신뢰도에 대한 수식
|
|
[표-2] Database transaction
|
Transaction ID |
Items |
|
100 |
A, C, D |
|
200 |
B, C, E |
|
300 |
A, B, C, E |
|
400 |
B, E |
- 최소 지지도 = 50% 이고 최소 신뢰도 80% 이상인 연관 규칙 찾기
- Join Step: Ck= LK-1 ⋈ LK-1 (⋈ = natural join)
- Prune Step: Ck의 모든 (k-1)-subset이 LK-1에 속하는 Ck만 보존
- 빈발 항목 탐색(frequent itemsets)
100 A D C [그림-2] 빈발 항목 탐색 과정
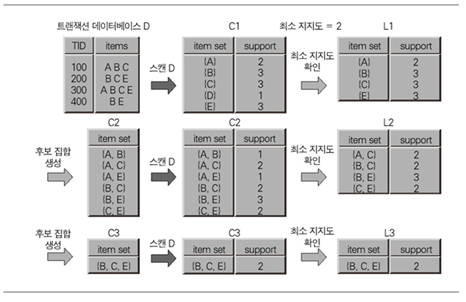
[표-3] 빈발 항목 집합
|
규칙 |
지지도(X Y) |
지지도 (X) |
신뢰도 |
|
{A} → {C} |
2 |
2 |
100 |
|
{B}→ {C} |
2 |
3 |
66.7 |
|
{B} → {E} |
3 |
3 |
100 |
|
{C} → {E} |
2 |
3 |
66.7 |
|
{B} → {C E} |
2 |
3 |
66.7 |
|
{C} → {B E} |
2 |
3 |
66.7 |
|
{E}→ {B C} |
2 |
3 |
66.7 |
|
{C} → {A} |
2 |
3 |
66.7 |
|
{C} → {B} |
2 |
3 |
66.7 |
|
{E} → {B} |
3 |
3 |
100 |
|
{E} → {C} |
2 |
3 |
66.7 |
|
{C E} → {B} |
2 |
2 |
100 |
|
{B E} → {C} |
2 |
3 |
66.7 |
|
{B C} → {E} |
2 |
2 |
100 |
Ⅲ. Apriori의 효율을 증대하는 기법
- Apriori 알고리즘은 구현하기 쉽고, 이해하기 쉬우며 어느 정도 만족할 만한 결과를 주기 때문에 자주 쓰이고 있으나, 후보 집합 생성시에 아이템의 개수가 많아지면 계산 복잡도가 엄청나게 증가하게 되는 문제 발생
- 해시 기반 기법(항목집합의 개수를 해싱하기): 해시 기반 기법은 후보 k-항목 집합 Ck(k>1)의 크기를 줄이는데 사용
- 트랜잭션 감소(다음 단계에서 스캔될 트랜잭션의 수를 줄임): 빈발 k-항목집합을 포함하지 않는 트랜잭션은 당연히 빈발(k+1)-항목집합을 포함하지 않으므로 해당 트랜잭션을 제거함
- 분할(후보 항목집합을 탐색하기 위한 데이터 분할): 분할기법은 빈발 항목집합을 발견하기 위하여 단지 두 번의 데이터베이스 스캔을 요구할 때 사용
- 샘플링(주어진 데이터의 일부분으로 마이닝): 주어진 데이터 D에서 임의의 샘플 S를 취한 후에 D대신에 S에서 빈발 항목 집합을 탐색

