B+Tree
태그 :
- 개념
- 키에 의해서 각각 식별되는 레코드의 효율적인 삽입, 검색과 삭제를 통해 정렬된 데이터를 표현하기 위한 트리자료구조
1. B+ Tree의 개요
가. B+Tree의 필요성
1) 데이터가 순차적으로 처리되어야 할 때는 트리 구조 내에서 노드 사이를 오르내리는데 많은 처리 시간이 필요하게 되는데 이런 경우 B+트리를 사용
- m-차수 트리의 한 종류로 노드의 Balance 를 맞춘 트리로 효율적인 균형 탐색 알고리즘을 제공함
- B 트리의 변형으로 인덱스 세트(index set)와 순차세트(sequence set)로 구성
나. B Tree와 차이점
- 인덱스 세트에 있는 키 값 : 리프 노드에 있는 키 값을 찾아가는 경로만 제공하기 위해서 사용
- 인덱스 세트의 노드와 순차 세트의 노드는 그 내부 구조가 서로 다름
. 인덱스 세트에 있는 노드 : 키 값만 저장, 리프 노드 : 키 값과 포인터가 함께 저장
- 순차 세트의 모든 노드가 순차적으로 서로 연결된 연결 리스트 (순차 접근이 효율적)
다. B Tree의 특징
- 루트는 0 또는 2에서 m개 사이의 서브트리를 가짐
- 루트와 리프를 제외한 모든 내부 노드는 최소 ⌈m/2⌉개, 최대 m개의 서브트리를 가짐
- 리프가 아닌 노드에 있는 키 값의 수는 그 노드의 서브트리 수보다 하나 적음
- 모든 리프 노드는 같은 레벨이며, 한 노드 안에 있는 키 값들은 오름차순
- 리프 노드는 모두 링크로 연결되어 있다
- 리프 노드의 키 값의 수는 [m/2] 이상이다
2.B+tree의 구성
가. B+ Tree의 구성 및 동작
- Index Set : 키, 포인터만 존재
. Index Set에 있는 Node는 Leaf를 찾아갈 수 있는 Key 값과 Pointer 값만 가지고 있음
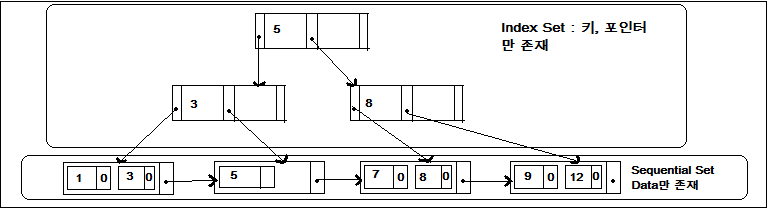
- Leaf Node관련 키값은 오름차순으로 정렬되어 있으며 삽입으로 인한 분기시 Sequence Set에 연결되면서 순차성 유지: 성능저하해결
- 삭제는 Leaf에서만 수행, 키 값은 Index Set에 유지하되 탐색 시에는 사용되지 않고 split값으로만 사용
나. B+tree의 data 구조/특징
1) 인덱스 세트 : 실제적인 키 값(Leaf node)를 찾아갈 수 있는 경로제공이 목적
- 인덱스 세트에 있는 노드는 키 값만 존재
- 각 노드는 키 값과 Sub-tree에 대한 포인터를 포함
- 인덱스 세트의 키 값은 Leaf node에 있는 키 갑을 찾아 갈 수 있는 직접 경로를 제공
2) 순차세트(Sequence Set)
- Leaf Node값은 오름차순으로 정렬되어 있으며, 삽입으로 인한 분기 시 Sequence Set에 연결되면서, 순차성 유지 : 성능 저하 해결
- 각각의 노드는 순차접근을 할 수 있도록 링크되어 순차접근이 용이
다. B+tree의 연산
1) 삽입
- B-트리와 유사하며, 리프의 오버플로우가 발생하면, 두 개의 노드로 분할하고 키 값들을 절반씩 분배해서 저장하며, 분할된 왼쪽노드에서 제일 큰 키 값을 부모 인덱스 노드로 저장
-> B 트리와의 차이점은 중간 키 값이 부모 인덱스 노드 뿐만 아니라 새로 분할된 노드에도 저장됨
2) 삭제
- 리프 노드에서만 삭제
ㆍ인덱스 노드에서는 분리자(separator)로 유지 (∵ 다른 키 값을 탐색하는데 분리 키 값으로만 사용)
<<키 값 43을 삭제한 이후의 트리>>
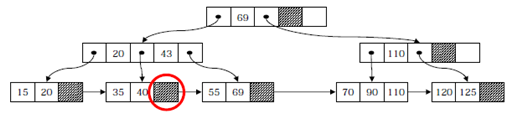
- 언더플로우로 인해 재분배가 일어나는 경우 : 인덱스 키 값 조정 (110 -> 90)
<<키 값 125의 삭제>>
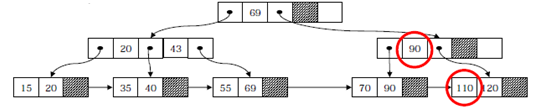
- 언더플로우로 인해 합병이 일어나는 경우 : 인덱스 키 값 삭제 (43)
<<키 값 55의 삭제>>
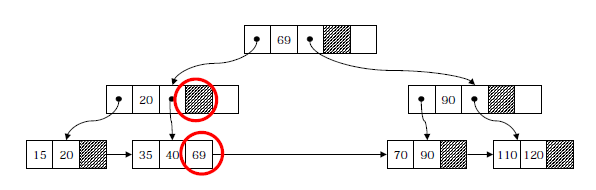
3. 기타 Tree(B*Tree, Red-Black Tree, Trie)
가. B* tree
- B-tree의 문제점(보조연산 필요)를 보완하기 위해서 B-tree를 약간 변형한 트리(보조연산 회수를 줄임)
- B-tree에 비해 공간활용도를 높일 수 있음(B-tree는 최소 1/2면 분열할 수 있지만, B* tree는 최소 2/3가 되어야 분열함)
- 노드의 분열을 줄여서 보조연산 회수를 감소시킴. 노드가 꽉 차면 분열하지 않고 형제 노드로 재배치(인접 노드 찰 때까지 지연 가능)
B*-Tree (Knuth 제안)
B-Tree의 단점
분열, 재분배, 합병 연산이 빈번 -> node 수 증가
각 node는 절반 정도가 Key값으로 채워짐
B*-Tree의 기본 Idea
Overflow 발생시 Split 대신 형제 node로 재분배
형제 node가 모두 Overflow이면 두 node를 세 node로 분할
=> 각 node는 2/3 정도가 채워짐
나. Red-Black Tree
- 각각의 노드가 레드 나 블랙 인 색상 속성을 가지고 있는 이진 탐색 트리
- 자료의 삽입과 삭제, 검색에서 최악의 경우에도 일정한 실행 시간을 보장 (worst-case guarantees)
- 루트 노드부터 가장 먼 경로까지의 거리가, 가장 가까운 경로까지의 거리의 두 배 보다 항상 작다
다. Trie
- 노드가 모두 포인터로 구성되며 해당 포인터 위치가 값을 의미
- 자료 탐색시 B+-tree와 같이 leaf node까지 가야만 key 값을 획득
- 찾는 key 값이 없을 경우 어느 level에서든지 끝낼 수 있어 key 값이 없는 경우의 탐색 효율 우수