- 데지덤
- 데이터베이스 개념
- 데이터베이스 개념
- DBMS
- DBS
- DBMS발전단계
- 데이터베이스개념
- 데이터
- 유일성
- DBMS
- 데이터독립성
- 데이터사전, 카탈로그
- 객체지향 DBMS
- 관계형DBMS
- 객체관계DBMS
- 데이터베이스 개발과운영
- 데이터베이스 분석,설계,구축 프로세스
- 클러스터링 테이블
- 데이터베이스 개념
- 데이터베이스 설계(1/2)
- 데이터표준
- 데이터, 정보, 지식, 지혜
- 릴레이션, 도메인, 튜플
- 데이터모델링
- 기본키
- 데이터모델링 개념
- 엔터티
- 속성
- 관계
- 식별자
- 개념적 데이터모델링
- 논리적 데이터모델링
- 물리적 데이터모델링
- 데이터표준
- 데이터베이스 설계(2/2)
- 프로세스 및 상관모델링
- 업무기능분해와 CRUD 매트릭스
- 정규화
- 정규화개요
- 함수종속성
- 이상현상
- 1차 정규화
- 2차 정규화
- 3차 정규화
- 보이스코드 정규화
- 4차 정규화
- 5차 정규화
- 반(역)정규화
- 반정규화개요
- DB물리설계
- DB 물리설계
- 무결성제약의 조건
- 프로세스 및 상관모델링
- 인덱싱과 DB프로그래밍
- 인덱스와 해싱
- B+Tree
- B-Tree
- T Tree구조
- R Tree구조
- 인덱스(Index)
- 해싱개요
- 관계연산
- 외부조인 & 세미조인
- Nested,Sort,Hash 조인
- 관계대수
- DB언어
- 데이터언어
- SQL
- SQL:1999/2003
- SQL 문장의 유형들
- SQL-집합, 서브쿼리, 아우터
- Embedded SQL
- Dynamic SQL
- SQL 부분범위처리
- SQL Full table scan
- SQL실행계획
- 인덱스와 해싱
- 데이터베이스 운영
- 트랜잭션
- 트랜잭션
- 2pc
- ACID
- ACID vs BASE
- 데이터베이스 복구
- 장애와 회복기법
- 데이터베이스 성능
- 데이터베이스 접근과정
- 데이터베이스 성능튜닝
- 데이터베이스 접근
- 병행제어(동시성제어)
- 동시성제어개요
- 잠금(Lock)
- 2PL
- Deadlock
- 낙관적제어(Validation)
- Isolation Level
- 트랜잭션
- 분석계 및 빅데이터기술
- 빅데이터기술
- NoSQL
- No-SQL 데이터모델링
- 빅데이터기술
- 데이터베이스 종류와 보안
- 데이터베이스 종류
- 멀티미디어DB
- 분산 데이터베이스
- XML 데이터베이스
- 공간 데이터베이스
- 메모리 데이터베이스
- 임베디드 데이터베이스
- 다중레벨 데이터베이스
- 이동객체 데이터베이스
- 모바일 데이터베이스
- 데이터베이스 종류
- 데이터베이스 개념
- 소지덤
- 소프트웨어
- 소프트웨어
- ISO25000, SQUARE
- ISO/IEC 12207
- Good S/W인증
- CMMi
- PSP/TSP
- ITSM
- ITIL
- 객체지향
- 모듈화, 결합도/응집도
- 3R
- UML
- SW 아키텍처
- 품질보증
- Peer Review
- 형상관리
- SW 신뢰성과 가용성
- SW 유지보수
- SOA
- OOP 5대원칙
- AOP 웹공학
- SW Metrics
- 코딩
- 코딩오류, 코드스멜, 리팩토링
- SWEBOK
- 스프링프레임웍
- SW비주얼라이제이션
- 소프트웨어
- 소프트웨어
- 네지덤
- 네트워크
- 네트워크
- 홈네트워크 미들웨어
- 성능향상 WLAN 표준
- CAN(Controller Area Network)
- NFC
- 망중립성
- 통신망
- WAVE
- WPAN
- Femtocell
- 세션계층
- 차량통신(V2X: Vehicle to Everything)
- DWDM
- 데이터링크 계층
- 저전력광역무선망(LPWAN)
- 6LoWPAN
- SDR
- 통신모델
- XMPP
- VLAN
- 스마트안테나
- 아날로그/디지털 신호
- 사물통신(사물인터넷, IoT: Internet of Things)
- CIDR
- 5G (IMT2020)
- 통신이론
- FBMC(Filter Bank Multi Carrier)
- CSMA/CA
- HSPA+
- TRS
- NOMA(Non Orthogonal Multiple Access)
- NFV(Network Function Virtualization)
- 변조 (Modulation)
- LTE
- 오버레이네트워크
- SDN(Software Defined Network)
- 응용통신
- TCP/IP 흐름제어
- CoIP
- VPN
- LTE-A(Advanced)
- 재난통신
- 인터네트워킹
- BCN
- QoS
- GSM/CDMA
- LIN(Local Interconnect Network)
- Ad-hoc
- 홈네트워크
- WiFi(WLAN)
- IVN(In Vehicle Network)
- SON
- MVNO
- TCP/IP
- DSRC
- WLAN
- NFV
- 전송계층
- NB-IoT(NarrowBand)
- TDMA, FDMA, CDMA
- 물리계층
- 소물통신(IoST: Internet of Small Things)
- IPv4/IPv6
- CR
- 다중화/다중접속
- CoAP
- NAT
- MIMO
- 통신기술
- MEC(Mobile Edge Cloud)
- IP Multicast
- LTE-A
- USB3.0
- 이동무선백홀
- CSMA/CD
- HSDPA
- M2M 외
- C-RAN(Cloud Radio Access Network)
- OpenFlow
- 오류정정기법 FEC, BEC
- 4세대 이동통신
- P2P
- 네트워크 슬라이싱(Network Slicing)
- LTE기반 국가재난안전무선통신망(PS-LTE)
- TCP / IP
- VoIP
- Tunneling
- LTE(Long Term Evolution)
- ITS/C-ITS
- 계층별 네트워크 프로토콜
- USN
- FTTH
- 이동통신
- FlexRay
- RFID
- ISM
- 기본통신
- V2V
- WBAN
- FMC, FMS
- 어플리케이션계층
- V2I(Vehicle to Infrastructure)
- 회선교환 vs 패킷교환
- 네트워크계층
- LoRa(Long Range)
- TDM, FDM, WDM
- SDN
- OSI 7 Layer
- LwM2M
- DHCP
- OFDM
- 변조/복조
- MQTT
- DNS
- Wibro
- 통신원리
- IBFD(In Band Full Duplex)
- 라우팅 프로토콜
- HSUPA
- IEEE1394
- Massive-MIMO
- 양자통신
- 네트워크 부호화
- WCDMA
- 웹가속기
- NFV(Network Function Visiulation)
- SDN(Software Defined Network)
- TCP/IP 혼잡제어
- Mobile IP
- CDN
- 5G/IMT-2020
- 국가재난안전통신망
- 계층별 장비
- 소프트스위치
- NMS
- 4G
- MOST
- OSI 7 Layer
- 무선매쉬네트워크
- 네트워크 기출문제
- 네트워크 감리사 기출문제[2/2]
- 네트워크 기술사 기출문제[2/2]
- 네트워크 감리사 기출문제[1/2]
- 네트워크 기술사 기출문제[1/2]
- 네트워크
- 네트워크
- 컴지덤
- 컴퓨터 구조
- 컴퓨터 구조
- VTL
- 멀티코어
- 프로세스 성능향상
- 병렬컴퓨터
- 길더의 법칙(Guilder's Law)
- 무어의 법칙
- 안드로이드 (Android)
- Fault Tolerant, High Availability
- Network Storage
- CPU 성능평가 (HW용량산정)
- CISC & RISC
- 폰 노이만형 아키텍처, 하버드 아키텍처
- 암달의 법칙 (Amdal's Law)
- JVM ,GC
- 차세대 저장장치
- 반도체 기억장치
- 파이프라인 해저드 (Pipeline Hazard)
- 명령어
- 파레토의 법칙
- 멧칼프의 법칙 (Metcalfe’s Law)
- 가상화
- 컴퓨터 구조
- 컴퓨터 구조
- 경지덤
- IT경영
- IT경영
- IT 거버넌스
- ISO 38500
- COBIT
- IT 경영전략
- SEM
- VBM
- 가상기업
- 전략수립도구
- EA
- EAP
- EA 참조 모델
- ISP/ISMP
- 전자정부표준프레임웍
- 정보기술아키텍처 성숙도 모델 v3.1
- ERP
- GSI
- ALM
- APM
- EAI
- B2Bi
- ITSM
- ISO20000
- ILM
- ITAM
- SAM
- ITO
- BPO
- Offshoring Outsourcing
- EO
- MDM
- MRO
- ECM
- RTE
- BPM
- Social BPM
- BRE
- BAM
- CRM
- CEM
- EIP
- X-Commerce
- IT투자분석
- BSC
- SLA, SLM, SOW
- BCM, BPC, DRS
- DRS
- SCM
- PLM
- CIM
- MES
- IT Compliance
- 바젤, 사베인즈 옥슬리
- 그린 IT
- 그린 IT 인덱스
- TRIZ
- Cobit 5.0
- 산업혁신 3.0
- Open Innovation
- IT경영
- IT경영
- 관지덤
- 프로젝트관리
- 프로젝트관리 개요
- 조직관리론
- 프로젝트 관리 개요
- 프로그램관리, 포트폴리오관리
- PMO
- PM
- 프로젝트 생애주기와 조직
- 프로젝트 관리 프로세스
- 프로젝트관리 영역
- 프로젝트 통합관리
- 프로젝트 범위관리
- 프로젝트 일정관리
- CPM
- CCM
- 프로젝트 원가관리
- 프로젝트 품질관리
- 프로젝트 인적자원 관리
- 프로젝트 의사소통 관리
- 프로젝트 위험관리
- 프로젝트 조달관리
- 프로젝트관리 기출문제
- 프로젝트관리 감리사 기출문제[1/4]
- 프로젝트관리 감리사 기출문제[2/4]
- 프로젝트관리 감리사 기출문제[3/4]
- 프로젝트관리 감리사 기출문제[4/4]
- 프로젝트관리 기술사 기출문제
- 프로젝트관리 개요
- 프로젝트관리
- 테지덤
- 테스트
- 테스트개요
- TDD
- SW 테스트의 개요
- V-Diagram
- SW 테스트의 유형
- SW 테스트 프로세스
- 프로젝트 단계별 테스트
- 통합테스트
- 성능테스트 – Little’s law 포함
- 단위 테스트
- 기능테스트 / 비기능테스트
- 시스템테스트
- 인수테스트
- 다양한 테스트 유형
- Black Box Text & White Box Test
- 경험기반 테스트
- 리스크 기반 테스트
- 유스케이스 테스트
- 경계값 분석(Boundary Value Analysis)
- 조건커버리지(Condition Coverage)
- 구조기반 테스트 – 테스트커버리지
- Mutation Test(비버깅)
- 유지보수 테스트
- 조합테스트
- 상태전이테스트
- 등가분할 테스트(Equivalence Partitioning)
- 결정 커버리지(Decision Coverage)
- 탐색적 테스팅
- 확인/리그레션테스트
- 분류트리기법테스트
- 결정테이블테스트
- 명세기반 테스트(Specification-based)
- 구문커버리지
- 테스트지원
- Peer Review
- Cyclomatic Complexity(McCabe)
- 리뷰
- Record & Replay
- 정적기법
- 테스트케이스(Test Case)
- 테스트인증평가
- TPI
- TMMi
- TMM(Test Maturity Model)
- SW오류종류 및 기타
- 테스트오라클
- 퍼지 테스트
- 테스트 주요용어 정리
- 퍼즈 테스팅(Fuzz Testing)
- 글로벌화 테스트
- 소프트웨어 오류
- 크라우드테스트
- Sanity Test
- 임베디드 테스트
- 테스트개요
- 테스트
- 돈지덤
- 비용산정
- 비용산정
- COCOMO2
- Function Point 절차 및 규칙 상세 2-2
- SW사업대가 산정법
- COCOMO
- Function Point 절차 및 규칙 상세 2-1
- Function Point 문제풀이
- Function Point(ISO/IEC 14143) 개요
- 비용산정
- 비용산정
- 분지덤
- 분석
- 분석
- Mobile Web 2.0
- 기계학습(Machine Learning)
- DW모델링
- SOAP
- 전문가시스템 (Expert System)
- EDW
- REST
- 트롤리 딜레마
- AJAX
- 인공지능 개념
- Map/Reduce
- 웹서버 부하분산
- NoSQL
- RDF
- DW 어플라이언스
- 퍼지
- WebOS
- Apriori 알고리즘
- 프로세스마이닝
- XQuery
- 몬테카를로 트리 서치 (Monte Carlo Tree Search)
- 데이터마이닝-신경망
- XML Schema
- KNN (K Near Neighborhood)
- 데이터마이닝-연관규칙(Association)
- HyWAI
- 로지스틱 회귀분석(Logistic Regression Analysis)
- OLAP
- Web2.0
- 유사도측정-유클리디안거리, 코사인유사도, 마할라노비스거리, 자카드계수
- ETT
- SOA
- 킬 스위치
- 데이터웨어하우스(DW)
- JSON
- 튜링 테스트
- Advanced Analytics
- Node.js
- 몽고 DB
- SPARQL
- 하둡
- Ontology
- 프로덕션시스템
- 웹마이닝
- DOM/SAX
- 연관분석
- 지지도/신뢰도/향상도
- XLL
- 은닉마르코프모델(HMM, Hidden Marcov Model)
- 기억기반추론(MBR)
- DTD
- 의사결정트리(Decision Tree)
- 데이터마이닝-클러스터 탐지
- WOA
- 회귀분석(Regression Analysis)
- BI, Bi2.0
- UDDI
- 추천엔진 (Recommendation Engine)
- ODS
- 웹서비스
- 아실로마 인공지능 원칙
- ESB
- 인공지능 역사
- HDFS
- 웹스토리지
- 카산드라
- Agent
- 빅데이터
- Semantic Web
- 인공지능
- 앙상블학습
- 텍스트마이닝
- XRX
- 군집화 K-means
- 데이터마이닝-분류
- XPATH
- 베이즈 정리
- 데이터마이닝-연속규칙
- XML
- 서포트 벡터 머신(Support Vector Machine)
- 데이터마이닝의 개요와 절차
- 분석
- 분석
- 시지덤
- 보안
- 보안
- IAM
- 생체인식
- OTP
- 빅데이터 보안
- SIEM
- 무선랜보안
- Secure Coding
- 세션 하이재킹
- IDS
- XSS
- APT 공격
- DOI, INDECS
- DRM
- 사회공학
- PMI
- EAM
- 접근통제
- VPN(IPSec, MPLS, SSL)
- 유비쿼터스 보안
- ESM
- 스마트그리드 보안
- Secure OS
- Forensic
- Firewall
- OWASP
- DDOS
- Watermarking
- CC
- 데이터베이스 보안
- PKI
- SSO
- AAA
- 암호화(DES, SEED, ARIA 등)
- RFID 보안
- Secure SDLC
- 클라우드 컴퓨팅 보안
- IPS
- SQL Injection
- 관리적보안, 물리적보안, 기술적보안
- 해킹
- SET
- MPEG21
- ISO27001
- 개인정보보호법
- 보안
- 보안
- 오지덤
- 운영체제
- 운영체제
- System Call
- Disk Scheduling
- Memory Mapped IO, I/O Mapped I/O
- Thrashing
- 메모리 관리기법
- Banker’s 알고리즘
- Race Condition
- 프로세스, 쓰레드
- 유닉스 파일시스템
- 가상메모리
- 메모리 인터리빙
- Locality
- 우선순위 역전
- 세마포어, 뮤텍스
- 인터럽트
- 모노리틱 커널, 마이크로 커널
- 버디메모리 할당
- RAID
- DMA (Cycle Stealing)
- Cache Memory
- 단편화
- CPU Scheduling
- 교착상태(Deadlock)
- Context Switching
- 운영체제
- 운영체제
- 운영체제
- 컨지덤
- IT컨설팅
- IT컨설팅
- Value Proposition
- McKinsey’s 7S’ model
- 시장 세분화
- 시나리오 기법(Scenario Planning)
- 3C분석
- TRL
- 특허
- Logic Tree
- Matrix 분석 기법
- 기술 수용 주기 분석-Chasm, 경쟁 포지셔닝 나침반
- 벤치마킹
- 제품개발의 손익분기점 분석(BEP)
- 마이클포터의 5 Forces 분석
- SWOT분석
- PI
- 정보기술 적용가능성분석
- TRIZ
- 게임 이론-동시적 게임의 손익행렬,전략적 게임보드
- 포트폴리오 관리기법-BCG Growth/Share Matrix
- Porter의 경쟁 전략
- Value Chain
- 사업의 경제성 분석
- 거시환경분석
- 가트너하이퍼사이클
- 상표권
- MECE/LISS
- 6 Sigma
- IT컨설팅
- IT컨설팅
- 유지덤
- UML/DF
- UML
- UML의 개요
- 객체지향
- 다형성
- 추상클래스
- 인터페이스
- UML
- UML 2.0
- UML의 확장
- 4+1 view
- UML 다이아그램
- Use Case 다이아그램 – 요구사항부터 구현까지
- Sequence 다이아그램
- Class 다이아그램
- 액티비티 다이어그램
- State Machine 다이어그램
- 클래스와 자바코드
- OCL (Object Constraint Language)
- DF
- 디자인패턴의 개요
- 상속과 위임
- Abstract Factory Pattern
- Factory Method Pattern
- Prototype Pattern
- Adapter Pattern
- Bridge Pattern
- Composite Pattern
- Decorator Pattern
- Facade Pattern
- Fly Weight Pattern
- Chain of Responsibility Pattern
- Command Pattern
- Interpreter Pattern
- Iterator Pattern
- Mediator Pattern
- Memento Pattern
- Observer Pattern
- State Pattern
- Strategy Pattern
- Template Method Pattern
- Visitor Pattern
- 헷갈리는 디자인패턴 간단한 구분
- 프레임워크, 디자인패턴, 아키텍처 스타일의 비교
- POSA(GoF 디자인패턴외)
- J2EE
- UML
- UML/DF
- 알지덤
- 알고리즘
- 자료구조
- 스택
- 트리 (Tree)
- 자료구조
- 연결 리스트 (Linked List)
- 그래프
- 알고리즘
- 철학자들의 만찬
- 문자열 탐색
- 순차 탐색 (Sequential Search)
- 힙 정렬 (Heap Sort)
- 삽입 정렬 (Insert Sort)
- 백트래킹 알고리즘
- 최단 경로 탐색 알고리즘
- 해시 탐색 (Hash Search)
- 계수 정렬 (Counting Sort)
- 합병 정렬 (Merge Sort)
- 선택 정렬 (Selection Sort)
- 알고리즘
- 논리회로
- 최소신장트리 알고리즘
- 이진 탐색 (Binary Search)
- 기수 정렬 (Radix Sort)
- 퀵 정렬 (Quick Sort)
- 버블 정렬 (Bubble Sort)
- 자료구조
- 알고리즘
- 신지덤
- 신기술
- 신기술
- 잊혀질 권리
- 소셜러닝
- 미라이 봇 넷
- S/W대가산정가이드-2013
- 압축표준(MPEC-H)
- SoC, SoB, SiP
- 초연결사회
- Bluetooth 5.0
- OVF
- SIEM
- FMEA
- FDS
- 하이퍼바이저
- 오픈소스(라이선스 비교)
- 스미싱
- PaaS-TA(파스타)
- 창조경제와 IT
- 빌딩로보틱스
- HW용량산정
- 에너지하베스팅
- NFC (Near Field Communication)
- Open API
- AMI
- CKAN
- e-Pub
- 마이그레이션
- 가시광통신
- 오픈스택
- 웹접근성 법제화
- FEMS
- ISO 29119
- Phishing
- Beacon
- ITS
- 플럽드 러닝
- LOD (Linked Open Data)
- Contents 2.0
- CASB (Cloud Access Security Broker)
- 증강인간/인지증강
- Telematics
- IoT 표준화 현황 및 추진전략
- 튤립버블, 알트코인
- SDN
- BIM
- Dublin core
- 사이버 망명
- SW기능 안정성
- IPCC
- 양자컴퓨터
- HTML 5
- Smart Work
- 클라우드 DR
- 증강현실 (Augmented Reality)
- LAS
- 4차산업혁명 보안
- 서비스 동향 및 사회적 이슈
- 썬더볼트 2
- ESS
- 2D 바코드(2D Barcord)
- 데이터 사이언티스트
- AUTOSAR
- EMS (Enterprise Mobile Solution)
- 소셜 CRM
- 린 스타트업
- 스마트그리드
- O2O(Online to Offline) 서비스
- FMEA
- IMS
- 표준화
- 드론 플랫폼
- TSM
- 에너지 그리드
- 메타버스
- NOSQL
- ISO26262
- EMR, HL7, PACS, DICOM
- 전력절감 컴퓨팅 기술
- 카파 아키텍쳐
- SNS
- 스낵컬처
- CKAN
- ENUM
- CPS(Cyber Physical System) 활용분야 및 최적화 전략
- 드론 보안
- NBA
- 하둡 3.0
- Streaming DBMS
- 에너지관리
- 제니비 연합
- 스턱스넷
- 정보보안 거버넌스 표준 ISO27014:2013
- 파티셔닝
- 문서중앙화
- 스마트 워치
- 탈중심웹 (Decentralized Web)
- BaaS
- 스마트팩토리
- Tactile Internet
- Wifi P2P WIFI Direct
- 하둡에코 (sqoop)
- SW 가시화
- 자율주행 자동차 - V2X
- IPv6보안
- FTL
- HDFS 2.0
- 디지털교과서
- 스파크
- 린 6 시그마
- ISO 26262
- 보안 MCU
- 레그테크
- MEAP
- 하둡에코 (Spark)
- 557(금융권)
- LKAS
- 지능형서비스로봇(URC)
- KWCAG 2.0
- Hadoop 2.0
- Ubiquitous Computing
- 아이디어 플랫폼
- 디지털 홀로그램
- 빅데이터 보안
- DMBok
- 디지털 큐레이션
- 하둡에코 (Chukwa),CPS(Cyber Physical System) [SAC]
- 망분리(지침과 금융권이슈)
- 자율주행 5대서비스,10대부품
- iOS (아이폰 OS)
- MMT
- Wear Leveling
- RTSP
- 핀테크
- 가상현실
- 오픈스택
- SWEBOK
- 소셜 TV
- IoT 보안 가이드라인
- 분리/분할발주 법령내용
- HEVC(MPEC-H Part2)
- User Interface
- MPEG
- 블루본
- RFID
- 운영감리
- 증강현실 (Augmented Reality)
- 감성 ICT 기술 및 산업동향
- 도커(Docker) [이컨엘엔허]
- 오픈소스 도입 전략 및 이슈
- 비싱
- 하둡에코 (YARN)
- PMO-기준(법령)
- MPEC-UD (User Description)
- OLED
- 가트너 10대기술
- Bluetooth 4.0
- OSGi
- IoT보안
- FTA
- VDI
- 가상화 (Type1/2, 대상)
- 카산드라 DB
- Open Cloud Foundry vs Open Shift(PaaS)
- CKAN
- 의무화 동향
- 그린인덱스
- GRC
- RFID
- NUI
- ESS
- CKAN, DKAN, OGPL, Socrata, Junar
- e-Discovery
- 클라우드테스트
- 오픈소스(오픈소스 도입 전략 및 이슈)
- UMB
- 개방형 IoT 플랫폼 (모비우스 기반)
- 반응형 웹(CSS3, 미디어쿼리)
- CEMS
- ISO 26000
- 개인정보 익명화
- WPAN (Wireless Personal Area Network)
- IPTV 보안
- MOOC
- 탈중심웹 (Decentralized Web)
- 재난통신
- SECaaS(Security As A Service)
- VR VS AR
- M2M
- IoT 플랫폼
- 안티 드론
- Wearable Computer(구글glass)
- 무선충전기술
- 3D TV
- 사이버 상조
- 자동차 사이버 보안 위협
- IoT (Internet of Things)
- SDX(SDN,SCDC,SDS,SDR)
- 린 6 시그마
- 스마트 카드
- 모바일클라우드보안
- 증강현실 (Augmented Reality)
- IP-USN
- 4차 산업혁명 [디생물]
- 블록체인 기반의 가상화폐
- 모바일 가상화
- 스마트 미터링
- ARC (Augmented Reality Continuum)
- 빅데이터 큐레이션
- ASIL
- emergent EA
- 하둡2.0, 하둡에코
- 그로스 해킹(코호트:(cohort)
- 마이크로 블로그
- 오픈소스 하드웨어
- FTA
- GPS
- 제조업 혁신 3.0
- 드론 정책
- gTLD
- 스마트 (파워)그리드
- 증강현실(AR)
- 컬럼기반 DB
- MirrorLink: CCC
- u-Health
- CCN
- 람다아키텍쳐
- SNG
- 디지털 발자국
- 오픈데이터 플랫폼
- DMB
- CPS(Cyber Physical System) 핵심기술
- AI 스피커
- SDP
- 하둡에코 (Pig)
- 악성코드패턴
- C-ITS
- 내부통제
- CISO
- 샤딩
- 모바일 오피스, 스마트 오피스
- 샌드박스
- WebRTC
- ISO 61508
- IoT 보안 인증제
- 제로UI
- 데이터 압축기법
- 하둡에코 (Kafka)
- Anonymous
- 자율주행 자동차 - WAVE
- DAP/LDAP
- 해커톤
- HDFS
- 디지털 홀로그래픽
- 마이핀
- 린 UI/UX
- 미라이 봇 넷
- 리걸테크(Legaltech)
- RCS
- 하둡에코 (Flume)
- 영상기기보안
- 자동차 자율주행 - ADAS
- OSS (Open Source Software)
- HTTP 적응적 스트리밍
- 빅데이터기술상세 Map/Reduce
- SVC
- SW BMT
- HCI
- AUTOSAR
- 도커(Docker) 아키텍처
- REBok
- 아키텍쳐 비즈니스 사이클
- 스마트팩토리
- 취약점 발견자 현상금
- 자율주행
- 안드로이드 아키텍처
- HEVC
- SSD
- RTLS
- 매그니튜드 익스플로잇 킷
- 가상현실
- 그로쓰해킹
- 디지털소멸
- 소셜커머스
- 보안 MCU
- SP인증
- MMT(MPEC-H Part1)
- User eXperience
- Node.js
- ZING
- PACS
- 분할발주
- Hazop
- 스트레처블 디스플레이 기술
- LXC (LinuX Container)
- 오픈소스(오픈소스화)
- 큐싱
- 하둡에코
- BYOD(CYOD, BYON)
- 압축표준(MPEG-21)
- ODF vs OOXML
- ISMS
- Zigbee
- SOAP
- CSB
- 초연결 사회, 데이터 거래소, Data 브로커
- GRID Computing
- 인티크레이션
- 무선전력전송기술
- 오픈스택 동향
- 정부 3.0
- HEMS
- 그린네트워킹
- Parming
- 비콘 플랫폼 (beacon platform)
- N-Screen
- WAVE
- 오픈데이터 플랫폼
- e-Book
- 클라우드 개발방법론
- BCI
- TPEG
- 모비우스(Mobius)
- LTE-A(광대역과 비교)
- BEMS
- ISO 26262
- 인터넷 윤리
- ISO 61508
- IPTV, Mobile IPTV
- 지능형 메모리 반도체(PIM)
- WebRTC
- 인포그래픽스
- DRaaS
- HMD (Head Mounted Display)
- LBS
- PLM
- 드론정책, 표준
- 3D Printer/4D
- 에너지하베스팅
- 3D Chip
- 잊혀질 권리
- ASPICE
- HCI (Human Computer Interaction)
- MEMS
- 린 UI/UX
- 마이크로 그리드
- 퍼블릭클라우드보안
- Hazop
- IPC
- 4차 산업혁명 [경계가 없어짐 / 융합]
- 안티드론
- BCI
- 마이크로그리드
- 라이프 로그(Life Log)
- 샤딩
- ISO 26262
- u-Learning
- 하둡
- 그로스 해킹(Growth Hacking)
- 소셜표준
- 자동차 자율주행
- 초연결 사회, 데이터 거래소, Data 브로커
- Femtocell
- 인더스트리 4.0
- 드론보안
- 스토리지 재해복구
- 엔터프라이즈 하둡
- 도메인테스트
- Appliance
- IVI/OAA/지니비
- Bio-Infomatics
- NFV
- 리플리케이션
- SNA
- 스마트교육
- LOD (Linked Open Data)
- DLNA
- CPS(Cyber Physical System) [SAC]
- 초연결 신뢰 네트워크
- Application Processor
- 하둡에코 (Hive)
- 코드 난독화(마스킹)
- 라이다(LiDAR, Light Detection And Ranging)
- RPD
- 칸반
- HDFS 1.0/HDFS 2.0 기능비교 (Hadoop2.0)
- 멀티모달 인터페이스
- STORM
- HTML 5
- ASIL
- IoT 보안 가이드라인
- 인슈어 테크
- Cloud Service Brokerage
- 하둡에코 (Storm)
- xDDOS(PDOS, DDOS, EDOS 등)
- C-V2X
- APT (Advanced Persistent Threat)
- ACID / BASE
- Hadoop 3.0
- U-City 보안
- 스마트팩토리
- 린 스타트업
- IoT보안(키교환)
- PMBok 5th, ISO 21500, 비교
- OTT
- 하둡에코 (Mahout)
- 보안거버넌스
- 자율주행
- CCL (Creative Commons License)
- DASH
- 3D D램
- SBC
- 크라우드 펀딩
- MR
- 오픈스택2
- 도커(Docker) 컨테이너 생성 관리 기술
- BABok
- Zero Client / Thin Client
- IoT 보안 인증제
- 보안사고(3.20, 6.25)
- 3D Audio(MPEC-H Part3)
- X Internet vs RIA
- H.264/AVC
- FTL(Flash Translation Layer)
- RSS
- CI
- HMD (Head Mounted Display)
- 사이버공격 역추적 기술동향
- 신기술
- 신기술
- 인지덤
- 인공지능
- 인공지능 개요
- 인공지능 개요
- 인공지능 역사
- 인공지능 평가 - 튜링 테스트
- 인공지능 아키텍처 - 규칙기반 모델(Rule-Based Model)
- 인공지능 아키텍처 - 전문가시스템 (Expert System)
- 인공지능 아키텍처 - 추천엔진 (Recmmendation Engine), 협업필터링
- 인공지능과 윤리 – 트롤리 딜레마
- 인공지능과 윤리 – 아실로마 인공지능 개발 원칙
- 인공지능과 윤리 – 킬 스위치
- 유한 오토마타
- 지능형 에이전트
- 유전자 알고리즘
- 인공지능 수학이론(통계와 확률)
- 상관분석(correlation analysis)
- 유사도측정(Similaraty Measure)
- 회귀분석(Regression Analysis)
- 로지스틱 회귀분석(Logistic Regression Analysis)
- 연관분석(Association Analysis)
- Apriori 알고리즘
- 앙상블학습(Ensemble learning)
- 머신러닝
- 기계학습(Machine Learning) 개요
- 의사결정트리(Decision Tree)
- KNN (K Near Neighborhood)
- 서포트 벡터 머신(Support Vector Machine)
- 베이즈 정리
- 클러스터링 K-means
- 밀도추정방식 DBSCAN Clustering
- 차원축소, Feature Extraction, PCA, ICA
- 은닉마르코프모델(HMM, Hidden Marcov Model)
- 몬테카를로 트리 서치 (MCTS, Monte Carlo Tree Search)
- Q-Learning
- 딥러닝
- 딥러닝 개요
- 신경망 알고리즘 원리 - 헵의 규칙
- 신경망 알고리즘 원리 - 퍼셉트론
- 신경망 알고리즘 원리 - 아달라인
- 신경망 학습 - 활성화 함수
- 신경망 학습 - Feed Forward Neural Network
- 신경망 학습 - 역전파(Backpropagation)
- 신경망 최적화 - 기울기 소실 (Vanishing Gradient Problem)
- 신경망 최적화 - 경사하강법(Gradient Descent)
- 학습 최적화 - 적합(overfitting), 부적합(underfitting)
- ANN, DNN
- CNN (Convolutional Neural Network)
- RNN (Recurrent Neural Network)
- LSTM, GRU
- RBN(Restrict Boltzmann Network)
- DBN(Deep Brief Network)
- DHN(Deep Hyper Net)
- DQN(Deep Q-Network)
- GAN(Generative Adversarial Network)
- 알고리즘 평가
- 혼동행렬 (Confusion Matrix)
- ROC 커브
- Cross Validation
- 통계적 가설검정
- 분야별 지능기술
- TF-IDF
- Tokenization, n-gram, 자연어처리
- Word2vec
- SNA
- 참고. AI플랫폼
- IBM Watson
- 텐서플로우(Tensor flow)
- Learning4J
- Mahout
- CNTK
- 인공지능 라이브러리 – MATLAB
- 인공지능 라이브러리 – Theano
- 인공지능 라이브러리 – Caffe
- 엑소브레인 (ExoBrain)
- 딥뷰 (Deepview)
- MS 코타나
- 인공지능 개요
- 인공지능
- 통지덤
- 통신이론
- 통신이론
- 통신이론
- 통신이론 – 통신원리
- 통신이론 – 통신기술
- 통신이론 – 통신기술 – 아날로그/디지털 신호
- 통신이론 – 통신기술 – 변조/복조
- 통신이론 – 통신기술 – 다중화/다중접속
- 통신모델
- 통신모델
- 통신모델 – OSI 7 Layer
- 통신모델 – OSI 7 Layer - 물리계층
- 통신모델 – OSI 7 Layer – 데이터링크 계층
- 통신모델 – OSI 7 Layer – 네트워크계층
- 통신모델 – OSI 7 Layer – 전송계층
- 통신모델 – OSI 7 Layer – 세션계층
- 통신모델 – OSI 7 – 프리젠테이션계층
- 통신모델 – OSI 7 – 어플리케이션계층
- 통신모델 – TCP/IP
- 통신망
- 통신망
- 통신이론
- 무선통신
- 기본통신
- 기본통신
- 기본통신 – WiFi(WLAN)
- 기본통신 – 성능향상 WLAN 표준
- 이동통신
- 이동통신
- 이동통신 – GSM/CDMA
- 이동통신 – 4G
- 이동통신 – 4G – LTE(Long Term Evolution)
- 이동통신 – 4G – LTE-A(Advanced)
- 이동통신 – 5G/IMT-2020
- 이동통신 – 5G/IMT2020 – 네트워크 슬라이싱(Network Slicing)
- 이동통신 – 5G/IMT2020 – SDN(Software Defined Network)
- 이동통신 – 5G/IMT-2020 – NFV(Network Function Visiulation)
- 이동통신 – 5G/IMT2020 – C-RAN(Cloud Radio Access Network)
- 이동통신 – 5G/IMT2020 – NOMA(Non Orthogonal Multiple Access)
- 이동통신 – 5G/IMT2020 – Massive-MIMO
- 이동통신 – 5G/IMT2020 – 이동무선백홀
- 이동통신 – 5G/IMT-2020 – FBMC(Filter Bank Multi Carrier)
- 이동통신 – 5G/IMT2020 – IBFD(In Band Full Duplex)
- 이동통신 – 5G/IMT2020 – MEC(Mobile Edge Cloud)
- 사물통신
- 사물통신(사물인터넷, IoT: Internet of Things)
- 사물통신 - MQTT
- 사물통신 - CoAP
- 사물통신 – XMPP
- 사물통신 – LwM2M
- 소물통신
- 소물통신(소물인터넷, IoST: Internet of Small Thinsg)
- 소물통신 – 저전력광역무선망(LPWAN)
- 소물통신 – 저전력광역무선망 – LoRa(Long Range)
- 소물통신 – 저전력광역무선통신 – NB-IoT(NarrowBand)
- 차량통신
- 차량통신(V2X: Vehicle to Everything)
- 차량통신 – V2I(Vehicle to Infrastructure)
- 차량통신 – V2I - DSRC
- 차량통신 – V2I - WAVE
- 차량통신 - V2V
- 차량통신 – IVN(In Vehicle Network)
- 차량통신 – IVN – CAN(Controller Area Network)
- 차량통신 – IVN - FlexRay
- 차량통신 – IVN – LIN(Local Interconnect Network)
- 차량통신 – IVN – MOST
- 차량통신 – ITS/C-ITS(Cooperative Intelligent Transport System)
- 재난통신
- 재난통신
- 재난통신 - 국가재난안전통신망
- 재난통신 - LTE기반 국가재난안전무선통신망(PS-LTE)
- 응용통신
- 응용통신
- 응용통신 – SDN(Software Defined Network)
- 응용통신 – SDN - OpenFlow
- 응용통신 – NFV(Network Function Virtualization)
- 양자통신
- 양자통신
- 기본통신
- 통신이론
B-Tree
태그 :
- 개념
- 데이터를 정렬하여 탐색, 삽입, 삭제 및 순차 접근이 가능하도록 유지하는 트리형 자료구조로. 트리의 루트로부터 하나의 노드에 이르는 모든 경로가 일정한 깊이를 유지하며 데이터의 접근시간이 동일함
1. Balanced Tree를 통한 균등한 응답속도 보장을 위한 탐색 트리, B-Tree 개요
가. B-Tree의 정의
- 데이터를 정렬하여 탐색, 삽입, 삭제 및 순차 접근이 가능하도록 유지하는 트리형 자료구조
* B 는 Balanced의 의미이며, leaf node가 한쪽 방향으로 쏠리는(skewed) 현상이 적음
나. B-Tree의 특징
- 각 노드는 1/2 이상 채워져야하며, 모든 leaf node는 같은 level에 있음
- 탐색, 추가, 삭제는 root node로부터 시작함
- 노드 내 값은 오름차순 유지
- 공백이거나 높이가 1이상인 m-원 탐색 트리(m-way search tree)
- 루트와 리프(leaf)를 제외한 내부 노드는 최소 [m/2], 최대 m개의 서브트리를 가지며, 적어도 [m/2]-1개의 키 값을 가짐 -> 적어도 반 이상이 키 값으로 채워져 있어야 한다
- 루트는 그 자체가 리프가 아닌 이상 적어도 두 개의 서브트리를 가짐
- 모든 리프는 같은 레벨에 있음 (균형 트리)
2. B-Tree의 구조와 장점 및 단점
가. B-Tree의 구조
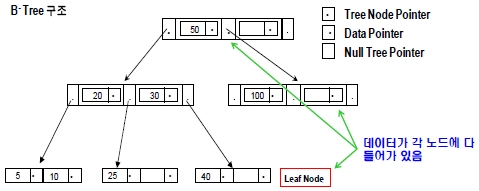
- In Order Tree Traversal 순서: 5, 10, 20, 25, 30, 40, 50, 100
나. B-Tree의 장점과 단점
|
장점 |
1) 삽입, 삭제 후에도 균형 트리 유지 2) 효율적인 알고리즘 제공 3) 저장 장치의 효율성 4) 균등한 탐색 속도 보장 가능 |
|
단점 |
1)노드의 삽입과 삭제 시 트리의 균형을 유지하기 위해 복잡한 연산(재분배, 합병)이 필요 2) 순차탐색 시에 inorder(중위) 순회로 비효율적 à B+ Tree 구조에서 leaf node간의 linked list로 순차 탐색 효율 향상됨 |
3. B-Tree와 B+tree의 비교 및 활용
가. B-Tree와 B+tree의 비교
|
구분 |
B-tree |
B+tree |
|
접근성 |
- 순차 접근이 어려움 - 탐색 중 원하는 키 값의 레코드 위치를 파악해야 함 |
- 순차 접근이 용이함 - 레코드의 위치는 leaf node에서만 파악됨 |
|
중복성 |
- 탐색 키의 중복성을 제거함 |
- Index Set와 Sequence Set에 중복성 존재 |
|
복잡성 |
- non-leaf node 크기가 더 크며 tree에 대한 저장공간 관리가 복잡함 |
- 모든 node 크기가 같으며 삭제될 node가 항상 lead node에 존재함 |
나. B-tree의 활용
- DBMS의 인덱스 자료구조로 활용 됨(B+tree 및 B*tree로 발전 적용)
- 검색엔진, 패턴 매칭 등 빠르면서도 성능이 일정하게 유지되는 탐색이 요구되는 분야에 활용됨
4. B-Tree 연산
가. 삽입
- 리프노드에 빈 공간이 있는 경우 : 단순히 빈 공간에 삽입하면 됨
- 오버플로 발생 시
1) 두 노드로 분열(split)
2) ⎡m/2 ⎤ 째의 키 값 -> 부모노드
3) 나머지는 반씩 나눔 (왼쪽, 오른쪽 서브트리)
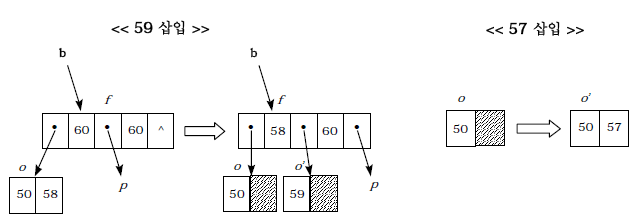
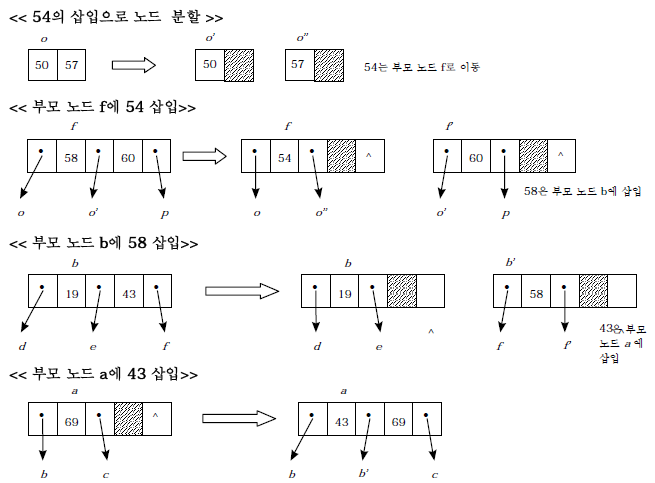
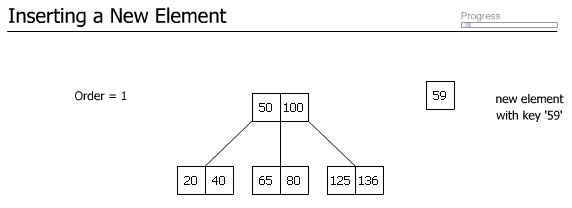
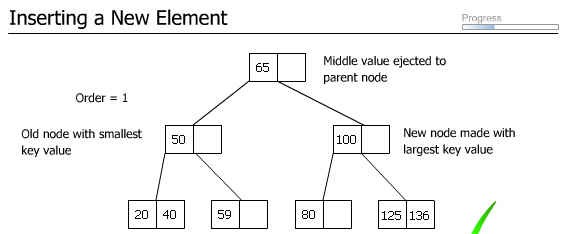
- 새로운 값 "59"가 추가된 경로를 간략히 설명
나. 삭제
- 리프노드에서 삭제
- 삭제키가 리프가 아닌 노드에 존재
. 후행키 값과 자리교환(후행키-항상 리프에)
. 리프노드에서 삭제
- 언더플로 : 키수 < ⎡m/2⎤ -1
. 재분배 (redistribution) : 최소키 수 이상을 포함한 형제노드에서 이동
(형제노드의 키 → 부모노드 → 언더플로 노드)
. 합병 (merge) : 재분배 불가능시 이용 (형제노드 + 부모노드의 키 + 언더플로 노드)