R Tree구조
태그 :
- 개념
- N차원의 공간 데이터를 효과적으로 저장하고 지리정보와 관련된 질의를 빠르게 수행 할 수 있는 자료구조
1. N차원 사각형 기반의 구조화된 자료구조, R-Tree
가. R-Tree의 정의
- N차원의 공간 데이터를 효과적으로 저장하고 지리정보와 관련된 질의를 빠르게 수행 할 수 있는 자료구조
나. R-Tree의 특징
M: 한 노드가 저장할 수 있는 최대 엔트리 수
m(<=M/2): 한 노드가 저장해야 되는 최소 엔트리 수
- 루트 노드가 아닌 노드는 최소 m, 최대 M개의 인덱스 엔트리와 자식 포인터를 포함한다.
- 루트 노드는 리프가 아닌 이상 최소 2개의 자식 노드를 갖는다.
- 모든 리프 노드는 최소 m, 최대 M개의 인덱스 엔트리를 포함한다
- 리프 노드에 있는 각 인덱스 엔트리는 객체 데이타를 실제 공간적으로 포함하고 있는 MBR과 이 공간 객체가 저장된 페이지 주소를 포함한다.
- 완전 균형 트리이다. 즉 모든 리프 노드는 같은 레벨에 있다.
2. R-Tree의 구조
가. R-Tree의 저장 단위인 MBR
1) 저장단위: 공간을 최소경계사각형(MBR: Minimum Bounding Rectangle)들로 분할하여 저장
2) MBB (Minimum Bounding Box) 라고도함
3) MBR의 종류
객체 MBR ; 객체 자체를 나타냄
- 리프노드 MBR ; 몇 개의 객체 MBR의 그룹을 표현하는 MBR
- 중간 MBR; 몇 개의 리프노드 그룹을 표현하는 MBR
나. MBR의 기본구조
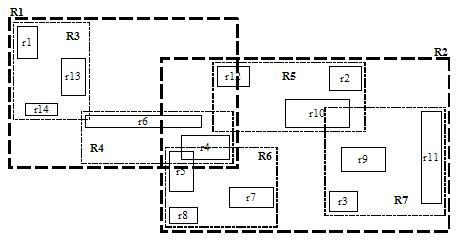
- M=3 m=2 인 명시적 MBR
수학적인 의미를 표현하기 위해 명시적 MBR로 구성
- 실제 R-tree는 리프노드와 중간 MBR에서의 합과 교차면적이 최소화 됨
- 2차 휴리스틱: 객체수의 제곱만큼 반복해서 최적화 수행)
다. R-Tree의 표현(나 항을 기반으로)
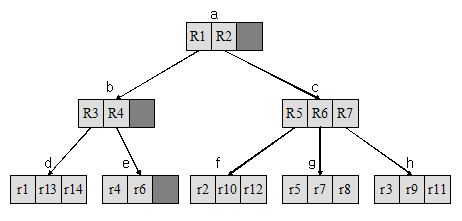
3. R-tree의 MBR관리와 탐색
가. R-Tree 의 MBR 관리
1) 삽입
- 데이타를 삽입할 적절한 리프 노드 선택. chooseLeaf() 알고리즘을 사용
- 리프 노드에 데이타 저장
- 선택된 리프 노드에 빈 공간이 있으면 새로운 엔트리 E를 저장. 빈 공간이 없는 경우 노드를 분할하여 E를 저장하고 트리를 조정
- 트리 재조정 : 데이타가 삽입된 경로를 따라 새로운 데이타 삽입으로 변경된 MBR들을 조정. 노드가 분할된 경우에는 새로운 MBR을 결정하고 그 부모 노드들을 따라가며 분할 된 노드에 대한 엔트리를 삽입. 이때 중간 노드에 자유 공간이 없으면 다시 분할이 계속될 수 있음
- 트리 높이 증가 : 만일 루트 노드가 분할되어야 하면 루트 노드를 분할하고 분할 된 두 노드에 대한 엔트리를 새로운 루트 노드를 만들어 저장. 이 경우 트리의 높이가 1 증가한다.
2) 삭제 :
- 리프 노드 탐색: 삭제할 데이타 객체를 포함하고 있는 리프 노드를 탐색.
- 해당 데이타 삭제: 리프 노드에서 해당 데이타 객체를 삭제.
- 언더플로 처리: 리프 노드의 엔트리 수가 m보다 작게 되면 언더플로가 발생하게 된다.
ㆍ언더플로가 발생한 노드를 삭제하고 그 노드의 모든 엔트리들을 트리에 다시 삽입
ㆍ 삭제로 인한 언더플로는 트리의 루트 방향으로 파급될 수 있음.
ㆍm개 이하의 엔트리를 갖는 중간 노드 역시 노드를 삭제하고 트리에 다시 삽입. 중간 노드를 재 삽입할 경우 이 노드는 원래의 레벨에 삽입되어야 함. 이때 MBR이 변하게 될 경우 트리의 루트까지 경로를 따라 MBR을 조정.
ㆍ 트리가 모두 조정된 뒤에 트리의 루트가 단지 하나의 자식만을 갖게 될 경우 루트의 자식 노드를 새로운 루트 노드로 만들고 기존의 루트 노드를 삭제. 이 경우 트리의 높이가 1 낮아짐.
나. R-Tree의 탐색
- 교차질의(Intersection): 모든 노드들은 질의입력 MBR과 자식 노드들의 MBR을 비교하여 교차되는 영역이 있는 자식 노드들에게만 질의를 전달함. 이러한 검색은 재귀함수로 구현 가능함
- 포함질의(Containment): 교차되는 영역이 있는 자식 노드가 아닌, 질의를 포함하는 자식 노드들만 검색
- 근접이웃질의(Nearest Neighbor): 점좌표와 거리를 입력 받아 특정 점좌표로부터 가장 가까운 거리에 위치한 데이터를 찾는 알고리즘
- R-TREE에서의 검색 경로는 중첩을 허용함으로 다중경로가 존재
4. R-Tree 및 R+Tree 알고리즘의 비교
가. R+Tree 알고리즘 이해
- R-Tree와 K-dimensional Tree의 중간형태로, 기본적인 구조와 연산은 R-Tree와 거의 동일하며, R+Tree는 내부 노드들의 중첩을 최소화하는 방법을 제시하여 삽입이나 삭제시 연산성능이 더 우수함
나. R+Tree와 R-Tree의 비교
- R-Tree의 Overlapping을 최소화하였고, 한 객체는 여러 단말 노드에 Duplicated되어 포함 될 수 있음
- 노드들이 서로 중첩되지 않으므로 Point Query 성능이 좋아지게 됨
- 중첩을 없애는 대신 중복저장으로 인해 Tree의 높이가 증가하여 공간 사용이 증가함
- MBR 객체들이 duplicated 되므로 R+Tree는 R-tree에 비해 크기가 더 커질 수 있음
- R+tree가 구조나 관리차원에서 R-Tree보다 더 복잡함
5. 결론
가. Projection 연산처리
- 특정시점질의, 시공간 범위 질의에 효과적
- 저장공간 감소
나. 활용분야
- GPS를 활용한 차량관리시스템, 항법시스템
다. 향후 발전 방향(다양한 질의 처리를 위해)
- Node 및 Tree의 새로운 구조 연구
- 여러 도메인에 따른 색인구조 및 알고리즘 고려(빈번한 업데이트 등)