Cyclomatic Complexity(McCabe)
태그 :
- 개념
- - 소프트웨어 복잡도 측정을 위해 사용되는 소프트웨어 지표 - Thomas McCabe에 의해서 개발됨 - McCabe 의 회전 복잡도는 상세 설계가 완료된 후부터 사용이 가능 하며, 프로그램의 제어 흐름도를 기반으로 분석 - 복잡도가 낮을수록 프로그램이 구조적으로 안정되었다는 의미이며, 높을수록 프로그램이 비 구조적이며 불안정하다는 의미
1. Cyclomatic Complexity의 개요
가. Cyclomatic Complexity의 정의
- 소프트웨어 복잡도 측정을 위해 사용되는 소프트웨어 지표
- Thomas McCabe에 의해서 개발됨
- McCabe 의 회전 복잡도는 상세 설계가 완료된 후부터 사용이 가능 하며, 프로그램의 제어 흐름도를 기반으로 분석
- 복잡도가 낮을수록 프로그램이 구조적으로 안정되었다는 의미이며, 높을수록 프로그램이 비 구조적이며 불안정하다는 의미
나. Cyclomatic Complexity의 공식
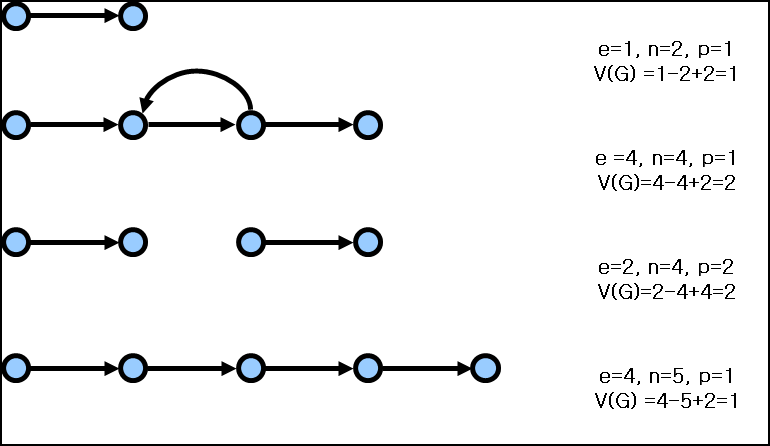
CC = V(G) = e – n +2p
- e : Flowgraph 내의 에지 수
- n : Flowgraph 내의 노드 수
- p : 연결되어있지 않는 Flowgraph 부분의 수
다. Cyclomatic Complexity의 예
2. Cyclomatic Complexity 계산 예(Another)
가. 계산
- 의사결정 수 + 1 또는 폐쇄영역(enclosed areas) + 1
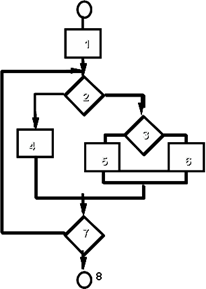 V(G) = 3+1 = 4
V(G) = 3+1 = 4
나. Cyclomatic Complexity: Flow Chart
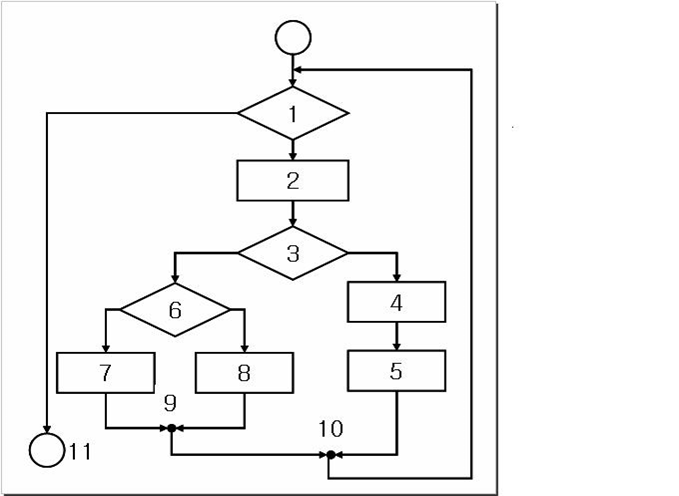
- V(G) is computed in one of three ways:
1. The number of regions corresponds to the cyclomatic complexity. (ex) V(G) = 4, ∵ Flow graph has 4 regions.
2. Cyclomatic complexity V(G), for a flow graph G, is defined as V(G) = E – N + 2,
Where E is the number of flow graph edges, and N is the number of flow graph nodes.
(ex) V(G) = 11 edges – 9 nodes + 2 = 4
3. Cyclomatic complexity V(G), for a flow graph G, is defined as V(G) = P + 1, where P is the number of predicate nodes contained in the flow graph G.
(ex) V(G) = 3 predicate nodes + 1 = 4.
predicate nodes: (1), (2,3), (6)
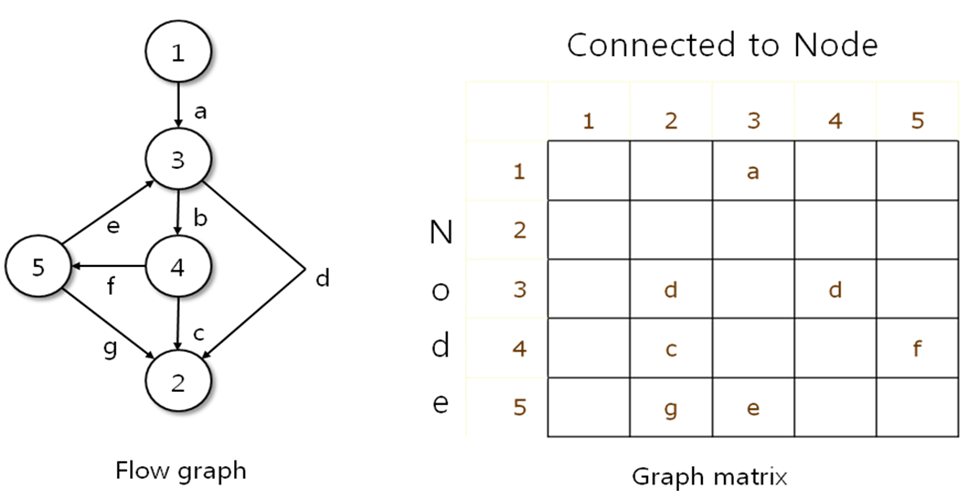
참고 : Graph Matrices
- a square matrix whose size is equal to the number of nodes on the flow graph.
- Each row and column corresponds to an identified node, and matrix entries correspond to connections (an edge) between nodes.
- Each node on the flow graph is identified by numbers, while each edge is identified by letters.
- To this point, the graph matrix is nothing more than a tabular representation of a flow graph.
- By adding a link weight to each matrix entry, the graph matrix can become a powerful tool for evaluating program control structure.
- The link weight provides additional information about control flow.
- In its simplest form, the link weight is 1 (a connection exists) or O (a connection does not exist).
- But link weights can be assigned other, more interesting properties:
- The probability that a link (edge) will be executed.
- The processing time expended during traversal of a link.
- The memory required during traversal of a link.
- The resources required during traversal of a link.
Control Structure Testing
< >Condition testing: a test case design method that exercises the logical conditions contained in a program moduleSimple conditionCompound conditionData flow testing: selects test paths of a program according to the locations of definitions and uses of variables in the programLoop Testing: a white-box testing that focuses exclusively on the validity of loop construct.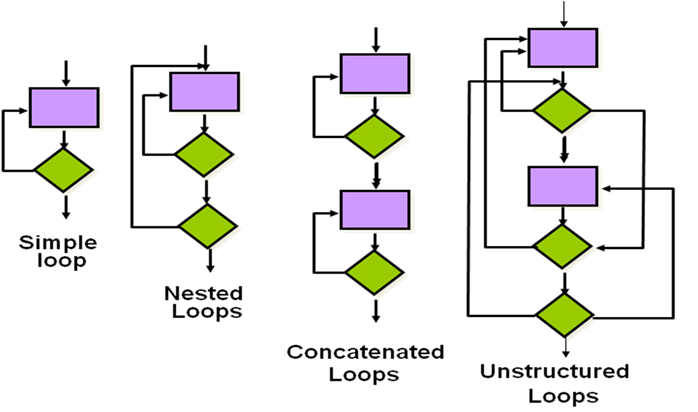
|
Loop |
내용 |
|
Simple Loops |
|
|
Nested Loops |
|

